Descripción

En el Reino OCI, la seguridad de la Cárcel IOI está estrictamente controlada. Hay ~N~ habitaciones en la Cárcel IOI, numeradas del ~1~ al ~N~. Hay ~N - 1~ pasajes que conectan las habitaciones. El pasadizo ~i~ (~1 \le i \le N - 1~) conecta la habbitación ~A_i~ y la habbitación ~B_i~ bdireccionalmente. Es posible pasar de cualquier habbitación a cualquier otra pasando por varios pasillos.

En la cárcel IOI hay ~M~ presos. Cada preso tiene un "número de identificación", que es un número entero entre ~1~ y ~M~ ambos inclusive. El dormitorio del preso ~j~ (~1 \le j \le M~) es la habbitación ~S_j~, y la sala de trabajo del preso ~j~ es la habbitación ~T_j~. Un preso puede trabajar en el dormitorio de otro preso. Sin embargo, no hay dos presos que compartan el mismo dormitorio, ni dos reclusos que compartan la misma sala de trabajo.

Una mañana, los ~M~ presos tienen que trasladarse de sus dormitorios a sus salas de trabajo. El Sr. PSN es el director de la cárcel IOI. Dará las siguientes instrucciones a los presos para que se trasladen.

La Dirección elige un prisionero y lo traslada de la sala actual a otra que esté conectada con la actual por un pasadizo. Para evitar la comunicación entre prisioneros, no está permitido trasladar al prisionero a una habitación en la que se encuentre otro prisionero.

Para poder empezar a trabajar lo antes posible, el Sr. PSN desea saber si es posible dar indicaciones para que cada preso no pase más de una vez por la misma habbitación (significa que cada preso toma el camino más corto).

Tarea

Escribe un programa que, dada la información de las habitaciones y los pasillos de la Cárcel de IOI y la información sobre los presos, determine si es posible mover a los presos de forma que cada uno de ellos tome el camino más corto.

Entrada

Un caso de prueba consta de ~Q~ escenarios, numerados de ~1~ a ~Q~. Para cada escenario se especifican los siguientes valores. Para conocer el rango de estos valores, consulte las Restricciones.

• El número ~N~ de habitaciones de la cárcel IOI.
• Información sobre los pasillos de la cárcel IOI ~(A_1, B_1), (A_2, B_2), ..., (A_{N-1}, B_{N-1})~.
• Número ~M~ de presos en la cárcel de IOI.
• Información sobre los dormitorios y las salas de trabajo de los presos ~(S_1, T_1), (S_2, T_2), ..., (S_M , T_M)~.

El formato de los datos de entrada es el siguiente. Los valores dados son todos enteros.

~Q~

(Entrada para el escenario 1)

(Entrada para el escenario 2)

...

(Entrada para el escenario ~Q~)

El formato de los datos de entrada para cada escenario es el siguiente. Para más detalles, véase Ejemplo de entrada y salida.

~N~

~A_1 B_1~

~A_2 B_2~

...

~A_{N-1} B_{N-1}~

~M~

~S_1 T_1~

~S_2 T_2~

... ~S_M T_M~

Salida

Escribe ~Q~ líneas en la salida estándar. La línea k-ésima (~1 \le k \le Q~) debe contener lo siguiente.

• Yes si es posible mover a los prisioneros para el escenario ~k~.
• No si no es posible mover a los prisioneros para el escenario ~k~.

Restricciones

• ~1 \le Q \le 1 000~.
• ~2 \le N \le 120 000~.
• ~1 \le A_i < B_i \le N~ (~1 \le i \le N - 1~).
• ~2 \le M \le N~.
• ~1 \le S_j \le N~ (~1 \le j \le M~).
• ~1 \le T_j \le N~ (~1 \le j \le M~).
• ~S_1, S_2, ... , S_M~ son diferentes entre sí.
• ~T_1, T_2, ... , T_M~ son diferentes entre sí.
• ~S_j~ ≠ ~T_j~ (~1 \le j \le M~).
• Es posible pasar de cualquier habbitación a otra pasando por varios pasillos.
• La suma de ~N~ para los escenarios ~Q~ es menor o igual a ~120 000~.

Subtareas

1. (5 puntos) ~A_i = i, B_i = i + 1~ (~1 \le i \le N - 1~).
2. (5 puntos) ~Q \le 20~, ~N \le 250~, ~M = 2~.
3. (16 puntos) ~Q \le 20~, ~N \le 250~, ~M \le 6~.
4. (28 puntos) ~Q \le 20~, ~N \le 250~, ~M \le 100~.
5. (12 puntos) ~Q \le 20~, ~M \le 500~.
6. (11 puntos) Es posible pasar de cualquier habbitación a cualquier otra habbitación atravesando como máximo ~20~ pasillos.
7. (23 puntos) No hay restricciones adicionales.

Ejempo de Entrada y salida

Ejmplo de Entrada #1

1
8
1 2
2 3
3 4
4 5
5 6
6 7
7 8
2
3 4
4 8

Ejemplo de Salida #1

Yes

Para esta entrada de ejemplo, si el director da las siguientes instrucciones, es posible mover a los prisioneros de modo que cada prisionero tome el camino más corto.

1. Mueve al prisionero 2 de la habbitación 4 a la habbitación 5.
2. Mueve al prisionero 1 de la habbitación 3 a la habbitación 4.
3. Mueva al prisionero 2 de la habbitación 5 a la habbitación 6.
4. Mueva al prisionero 2 de la habbitación 6 a la habbitación 7.
5. Mueva al prisionero 2 de la habbitación 7 a la habbitación 8.

Por lo tanto, salida es Yes (Sí). La estructura de la cárcel para esta entrada de ejemplo es la siguiente.

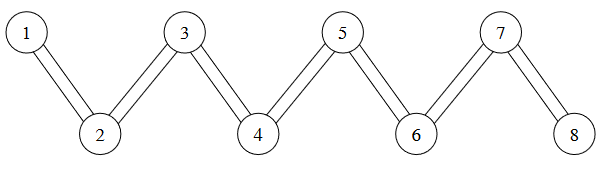
Esta entrada de ejemplo satisface las restricciones de todas las subtareas.

Ejmplo de Entrada #2

2
7
1 2
2 3
3 4
4 5
3 6
6 7
2
4 1
5 7
4
1 2
1 3
1 4
3
2 3
3 4
4 2

Ejemplo de Salida #2

Yes
No

Hay ~Q = 2~ escenarios. Para el Escenario 1, si el director da las siguientes instrucciones, es posible mover los prisioneros de modo que cada prisionero tome el camino más corto.

1. Mover al prisionero 1 de la habbitación 4 a la habbitación 3.
2. Mueve al prisionero 1 de la habbitación 3 a la habbitación 2.
3. Mueva al prisionero 2 de la habbitación 5 a la habbitación 4.
4. Mueva al prisionero 2 de la habbitación 4 a la habbitación 3.
5. Mueva al prisionero 2 de la habbitación 3 a la habbitación 6.
6. Mueva al prisionero 1 de la habbitación 2 a la habbitación 1.
7. Mueva al prisionero 2 de la habbitación 6 a la habbitación 7.

Sin embargo, para el Escenario 2, no es posible mover a los prisioneros de forma que cada uno de ellos tome el camino más corto.

Por lo tanto, la primera línea de salida debe ser Yes, y la segunda línea de salida debe ser No.

Este ejemplo de entrada satisface las restricciones de las subtareas ~3, 4, 5, 6, 7~.

Ejmplo de Entrada #3

3
3
1 2
2 3
2
2 1
3 2
7
1 2
2 3
3 4
4 5
5 6
6 7
3
1 3
4 2
2 5
8
1 2
2 3
3 4
4 5
5 6
6 7
7 8
4
1 5
2 6
3 7
4 8

Ejemplo de Salida #3

Yes
No
Yes

Este ejemplo de entrada satisface las restricciones de las subtareas ~1, 3, 4, 5, 6, 7~.