Torres de Cubos
Teniendo varios cubos disponibles, Lidia y Leonardo decidieron construir edificios uniendo dos o más torres. Las torres se obtuvieron colocando los cubos uno encima del otro. La altura de una torre está dada por el número de cubos a partir de los cuales se forma.
Los edificios construidos fueron colocados en línea, uno al lado del otro formando así una calle, sobre la cual caminarán los dos niños.
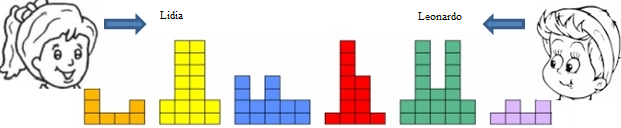
Para la numeración de los edificios Lidia y Leonardo, establecieron las siguientes reglas:
- Lidia comienza desde un extremo de la calle y Leonardo desde el otro extremo; cada uno de ellos cruza la calle por completo, pasando por la derecha de cada edificio.
- Lidia pega en cada edificio una nota que escribe la altura de las torres desde las cuales está construida, en el orden en que las ve cuando pasa a su derecha (por ejemplo, para la imagen de arriba, Lidia pegará una nota en el primer edificio que escribirá el número
porque, la primera torre consta de
cubos, las siguientes dos torres de este edificio están hechas de un cubo y la cuarta torre está hecha de
cubos);
- Leonardo hará lo mismo, pero comienza la caminata desde el otro extremo de la calle. En el ejemplo de la imagen, pegará en el primer edificio una nota que escribe el número
que encuentra.
Al final de la caminata, Lidia y Leonardo se dan cuenta de que hay edificios en los que se adjuntaron ambas tarjetas con números idénticos.
Tarea
Para un V dado resuleva las siguientes tareas:
Si
, ¿cuál es la altura de la torre más alta y cuál es el número de edificios que tienen tal torre en su construcción?
Si
, ¿cuál es el número de edificios en los que los dos niños pegaron las tarjetas con números idénticos?
Si
, ¿cuál es el menor número de cubos necesarios para completar los edificios para que, en cada edificio, la nota que peque Lidia contenga el mismo número que el que Leonardo pegará? Los cubos desde los cuales se construyó originalmente el edificio no se pueden mover.
Si , debe darle respuesta a las tres tareas anteriores.
Datos de entrada
La entrada estándar leerá desde la primera línea un número natural , que representa el número de edificios en la calle, y de las siguientes líneas
un número natural con todas las cifras distintas de cero, que representan los números escritos por Lidia en las notas, en el orden en que estaban unidos a él en edificios.
Datos de salida
En la salida estándarEn se escribirán en la primera línea dos números naturales separados por un solo espacio que representa, en orden, los valores requeridos en el requisito . En la segunda línea se escribirá un número natural, mayor o igual a cero, que representa la respuesta al requisito
. En la tercera línea se escribirá un número natural, mayor o igual a cero, que representa la respuesta al requisito
.
Restricciones y especificaciones
- Cada edificio consta de no más de
torres, y la altura de cada torre se expresa con una cifra distinta de cero.
- Para la solución correcta del requisito
se otorga el
% si V = 1.
- Para la solución correcta del requisito
se otorga el
% si V = 2.
- Para la solución correcta del requisito
se otorga el
% si V = 3.
- Para la solución correcta de todos los requisitos se otorga el
si V = 4.
Ejemplo de Entrada
6 4
3112
2772
42422
1741
27372
1212Ejemplo de Salida
7 3
2
8Explicación
Como V = 4 se debe de resolver los tres requisitos
La torre más alta consta de cubos. Hay
edificios que tienen torres con esta altura en su construcción, en los que Lidia pega los números:
,
y
. Leonardo pega a los edificios las notas con los números:
,
,
,
,
y
. Dos de estos edificios recibieron los mismos números de Lidia:
y
. El valor determinado según el requisito
es
. Agregue un cubo al edificio con el número
,
cubos al que tiene el número
,
cubos al edificio con el número
y
cubos al que tiene el número
.
Explicación
Comments