Bitman tiene un arreglo de ~n~ elementos, ~a=[a_0, a_1, ..., a_{n-1}]~. Para algun subarreglo, ~b~, de ~a~, defininimos ~G(b)~ como:

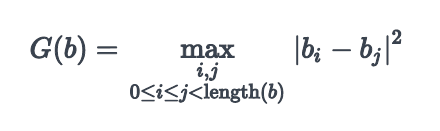
donde ~length(b)~ es la longitud de ~b~, y ~b_i~ es el ~i^{th}~ elemento de ~b~.

Bitman calcula la suma de ~G(b)~ para todos los posibles subarreglos ~b~ de ~a~ calculando

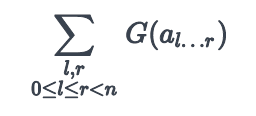
donde ~a_{l...r}~ es el subarreglo de ~a~ del indice ~l~ al indice ~r~.

Dado ~a~, imprima la suma descrita arriba modulo ~2^{64}~

Entrada

La primera linea de la entrada contiene un entero ~n~ (el tamaño del arreglo). La segunda línea contiene ~n~ enteros separados por espacio los que representan respectivamente los valores de ~a_0, a_1, ..., a_{n-1}~

Restricciones

• ~1 \leq n \leq 2.10^5~
• ~1 \leq a_i \leq 2.10^5~

Salida

Imprima un entero denotando la suma, modulo ~2^{64}~.

Ejemplo # 1 de Entrada

 5
 1 2 3 4 5

Ejemplo # 1 de Salida

50

Explicación # 1

~a_{1...1} = [1]~ ~ ~ ~ ~ ~ ~ ~G(a_{1...1})=0~

~a_{1...2} = [1,2]~ ~ ~ ~ ~ ~ ~ ~G(a_{1...2})=1~

~a_{1...3} = [1,2,3]~ ~ ~ ~ ~ ~ ~ ~G(a_{1...3})=4~

~a_{1...4} = [1,2,3,4]~ ~ ~ ~ ~ ~ ~ ~G(a_{1...4})=9~

~a_{1...5} = [1,2,3,4,5]~ ~ ~ ~ ~ ~ ~ ~G(a_{1...5})=16~

~a_{2...2} = [2]~ ~ ~ ~ ~ ~ ~ ~G(a_{2...2})=0~

~a_{2...3} = [2,3]~ ~ ~ ~ ~ ~ ~ ~G(a_{2...3})=1~

~a_{2...4} = [2,3,4]~ ~ ~ ~ ~ ~ ~ ~G(a_{2...4})=4~

~a_{2...5} = [2,3,4,5]~ ~ ~ ~ ~ ~ ~ ~G(a_{2...5})=9~

~a_{3...3} = [3]~ ~ ~ ~ ~ ~ ~ ~G(a_{3...3})=0~

~a_{3...4} = [3,4]~ ~ ~ ~ ~ ~ ~ ~G(a_{3...4})=1~

~a_{3...5} = [3,4,5]~ ~ ~ ~ ~ ~ ~ ~G(a_{3...5})=4~

~a_{4...4} = [4]~ ~ ~ ~ ~ ~ ~ ~G(a_{4...4})=0~

~a_{4...5} = [4,5]~ ~ ~ ~ ~ ~ ~ ~G(a_{4...5})=1~

~a_{5...5} = [5]~ ~ ~ ~ ~ ~ ~ ~G(a_{5...5})=0~

La suma de esos valores es ~0+1+4+9+16+0+1+4+9+0+1+4+0+1+0=50~, entonces imprima como la respuesta el resultado de ~50~ mod ~2^{64}=50~.

Ejemplo # 2 de Entrada

 4
 3 1 4 2

Ejemplo # 2 de Salida

44

Explicación # 2

~a_{1...1} = [3]~ ~ ~ ~ ~ ~ ~ ~G(a_{1...1})=0~

~a_{1...2} = [3,1]~ ~ ~ ~ ~ ~ ~ ~G(a_{1...2})=4~

~a_{1...3} = [3,1,4]~ ~ ~ ~ ~ ~ ~ ~G(a_{1...3})=9~

~a_{1...4} = [3,1,4,2]~ ~ ~ ~ ~ ~ ~ ~G(a_{1...4})=9~

~a_{2...2} = [1]~ ~ ~ ~ ~ ~ ~ ~G(a_{2...2})=0~

~a_{2...3} = [1,4]~ ~ ~ ~ ~ ~ ~ ~G(a_{2...3})=9~

~a_{2...4} = [1,4,2]~ ~ ~ ~ ~ ~ ~ ~G(a_{2...4})=9~

~a_{3...3} = [4]~ ~ ~ ~ ~ ~ ~ ~G(a_{3...3})=0~

~a_{3...4} = [4,2]~ ~ ~ ~ ~ ~ ~ ~G(a_{3...4})=4~

~a{4...4} = [2]~ ~ ~ ~ ~ ~ ~ ~G(a_{4...4})=0~

La suma de esos valores es ~0+4+9+9+0+9+9+0+4+0=44~, entonces imprima el resultado de ~44~ mod ~2^{64}=44~ como la respuesta.