Los azucareros del centro en sus estudios de la teoría de grafos estudiaron las definiciones de los siguientes términos:

• Camino Simple: Un camino que no contenga cualquier nodo o arco más de una vez.

• Ciclo simple: Un ciclo que no contenga cualquier nodo o arco más de una vez.

• Árbol: Un grafo conectado no direccional con ningún ciclo simple.

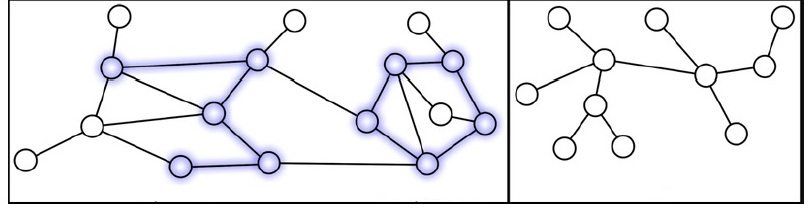
En la figura de abajo vista de izquierda a derecha, el primer subgrafo sombreado que aparece es un camino simple, el segundo subgrafo sombreado es un ciclo simple, mientras que el grafo de más a la derecha es un árbol.

Dado un árbol con arcos con peso con ~n~ nodos numerados de ~1~ a ~n~ donde cada nodo es rojo o negro, encontrar e imprimir la suma de los pesos de todos los caminos simples de un nodo rojo a un nodo negro en el árbol.

Entrada

La primera línea de la entrada contiene un entero, ~n~, denotando el número de nodos en el árbol. La segunda línea contiene n enteros binarios separados por espacio describiendo los respectivos valores de ~c_1, c_2, ..., c_n~, donde un ~c_i~ con valor de ~0~ denota que el nodo ~i~ es rojo y un valor de ~1~ denota que es negro. Cada una de las ~n-1~ subsecuencias contienen tres enteros separados por espacio describiendo los respectivos valores de ~u, v~ y ~w~ que definen un arco con peso w conectando los nodos ~u~ y ~v~.

Salida

Imprima un entero simple que represente a la suma de los pesos de todos los caminos simples únicos de un nodo rojo a un nodo negro en el árbol.

Restricciones

• ~1 \le n \le 10^5~

• Cada ~c_i~ está en el conjunto ~{0,1}~, donde ~0~ denota rojo y ~1~ denota negro.

• ~1 \le u,v \le n~

• ~1 \le w \le 10^6~

Ejemplo de Entrada

4
0 0 1 1 
1 2 1
2 3 2 
2 4 2

Ejemplo de Salida

 10

Explicación del ejemplo: En este ejemplo, ~n=4~, los nodos ~1~ y ~2~ son rojos, y los nodos ~3~ y ~4~ son negros. El dibujo de abajo describe el árbol dado y todos sus caminos simples únicos de un nodo rojo a uno negro:

Hay cuatro de tales caminos

1. Camino \(2 → 3\), el cual tiene un peso total de ~2~.

2. Camino de \(2 → 4\), el cual tiene un peso total de ~2~.

3. Camino \(1 → 2 → 3\), el cual tiene un peso total de ~1+2=3~.

4. Camino \(1 → 2 → 4\), el cual tiene un peso total de ~1+2=3~.

Entonces la longitud total de todos los caminos simples únicos es ~2+2+3+3=10~.