Usted tiene un árbol orientado con ~n~ nodos numerados ~0,1,2,...,n-1~ que tiene como raíz al nodo ~0~. Un árbol orientado significa que todos los arcos son dirigidos y apuntan desde el nodo raiz. Por ejemplo, el diagrama de abajo describe un árbol orientado con ~n=8~

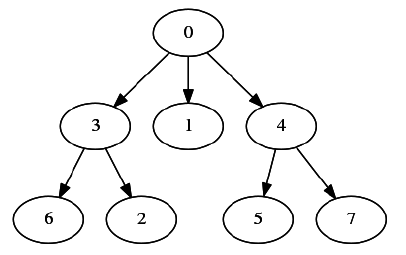
Definiremos entonces:

• ~level(u)~ como la distancia en arcos entre el nodo ~u~ y el nodo raíz.

• La altura, ~h~, del árbol como el máximo ~level~ de cualquier nodo.

• ~subtree(u)~ como el conjunto de los nodos alcanzables desde el nodo ~u~ (esto incluye al nodo ~u~).

• ~f(l,k)~ como el número de nodos ~v~ tal que ~subtree(v)~ contiene al menos ~k~ nodos cuyo ~level~ es ~l~.

Más formalmente, suponga que nosotros definimos ~S_{v,l}~ como el conjunto {~u \in subtree(v) | level(u)=l~}. Entonces ~f(l,k)~ es el número de nodos tal que ~|S_{v,l}| >= k~.

Dado los números ~a_0,a_1,a_2,...,a_h~ encuentre e imprima el resultado de: ~\sum_{i=0}^{h} f(i, a_i)~

Entrada

La primera línea de la entrada contiene dos enteros separados por espacio describiendo los valores respectivos de ~n~ (el número de nodos en el árbol) y ~h~ (la altura del árbol). La segunda línea contiene ~n-1~ enteros separados por espacio describiendo los valores respectivos de ~p_1, p_2,...,p_{n-1}~, donde cada ~p_i~ es el identificador del nodo padre de ~i~. En otras palabras, cada ~p_i~ define un arco orientado de ~p_i~ a ~i~. La tercera línea contiene ~h+1~ enteros separados por espacio describiendo a los respectivos valores de ~a_0, a_1, ..., a_h~.

Restricciones

• ~1 \leq n \leq 5.10^5~
• ~0 \leq h < n~
• ~0 \leq p_i < n~
• ~0 \leq a_i \leq n~
• se garantiza que la entrada define a un árbol orientado.
• ~h~ es la altura del árbol.

Salida

Imprima un entero denotando ~\sum_{i=0}^{h} f(i, a_i)~

Ejemplo de Entrada

5 2
0 0 2 2
0 1 2

Ejemplo de Salida

10

La siguiente figura describe el arbol del ejemplo de entrada:

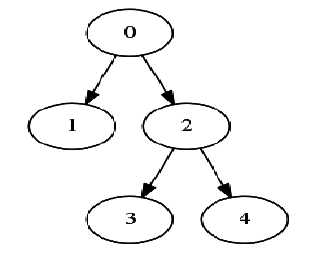
Los ~levels~ de los nodos son los siguientes

|----------|---|---|---|---|---| | u | 0 | 1 | 2 | 3 | 4 | | level(u) | 0 | 1 | 1 | 2 | 2 |

Ahora,

• ~f(0,a_0)=f(0,0)=5~ ya que los nodos ~0,1,2,3~ y ~4~ contienen al menos ~a_0=0~ nodos en su subarbol cuyo ~level~ es ~0~.
• ~f(1,a_1)=f(1,1)=3~ ya que los nodos ~0,1~ y ~2~ contienen al menos ~a_1=1~ nodos en su subarbol cuyo ~level~ es ~1~.
• ~f(2,a_2)=f(2,2)=2~ ya que los nodos ~0~ y ~2~ contienen al menos ~a_2=2~ nodos en su subarbol cuyo ~level~ es ~2~.

Asi, la respuesta es ~5+3+2=10~.