Puentes aéreos
En Cosmosland, hay una famosa universidad llamada Universidad de Sagan. Todos los estudiantes se alojan en un edificio de dormitorios de pisos. Este año, la universidad ha terminado de construir un nuevo edificio de dormitorios de
pisos.
Hay puentes aéreos entre los dos edificios. El
-ésimo puente aéreo está montado a la altura del piso
. Cada piso de cada edificio solo está conectado exactamente a un puente aéreo a través de un túnel especial. El piso
del edificio antiguo solo está conectado al
-ésimo puente aéreo, y el piso
del nuevo edificio solo está conectado al
-ésimo puente aéreo. Para más detalles, las ilustraciones se proporcionarán en la explicación del ejemplo.
La universidad quiere trasladar a todos los estudiantes al nuevo edificio. Los estudiantes de cada piso del edificio antiguo serán reubicados a un piso en el edificio nuevo. No se trasladarán dos pisos del edificio antiguo al mismo piso del edificio nuevo. En otras palabras, la universidad quiere calcular una permutación
que denota que los estudiantes del piso
en el edificio antiguo serán reubicados en el piso
en el nuevo edificio.
Por razones de seguridad, la universidad quiere imponer las siguientes restricciones para cada nivel en la reubicación:
Los estudiantes de cada piso del edificio antiguo irán al único puente aéreo conectado, luego caminarán a lo largo del puente aéreo y luego subirán a un piso en el nuevo edificio que está conectado al puente aéreo.
El piso anterior en el edificio antiguo y el piso nuevo en el edificio nuevo no deben ser ambos más altos o más bajos que el puente aéreo de conexión.
O, más formalmente, para cada i, se deben cumplir todas las condiciones siguientes:
- Si
, entonces debe darse el caso de que
.
- Si
, entonces debe darse el caso de que
.
Ahora, la universidad es curiosa: ¿cuántas permutaciones diferentes son posibles? Dado que pueden ser muchas, sienten curiosidad por el resultado módulo .
Formato de entrada
Las líneas se dan en el siguiente formato:
N K
H [1] H [2] .. H [K]
A [1] A [2] A [3] .. A [N]
B [1] B [2] B [3] .. B [N]Formato de salida
Una sola línea que consta del número de posibles permutaciones, módulo 1,000,000,007. Entrada de muestra 1
Restricciones
Para todas las subtareas:
Todos los valores de
son diferentes.
contiene todos los números del
al
al menos una vez.
contiene todos los números del
al
al menos una vez.
Para cada puente aéreo, el número de pisos conectados en el edificio antiguo es igual al número de pisos conectados en el edificio nuevo.
Subtareas
Subtarea 1 (10 puntos):
Subtarea 2 (14 puntos):
Subtarea 3 (22 puntos):
Subtarea 4 (34 puntos):
- Para cada
, \(H [A [i]] ≠ i\)
- Para cada
, \(H [B [i]] ≠ i\)
Subtarea 5 (20 puntos):
- Sin restricciones adicionales.
Ejemplos
Ejemplo de entrada 1
6 1
3
1 1 1 1 1 1
1 1 1 1 1 1Ejemplo de salida 1
36Explicación del ejemplo 1
Hay pisos y
puente aéreo ubicado a la altura del piso
. Cada piso, tanto en los edificios nuevos como en los antiguos, está conectado al puente aéreo.
Este ejemplo se ilustra con la siguiente imagen. El edificio de la izquierda representa el edificio antiguo, mientras que el de la derecha representa el edificio nuevo.
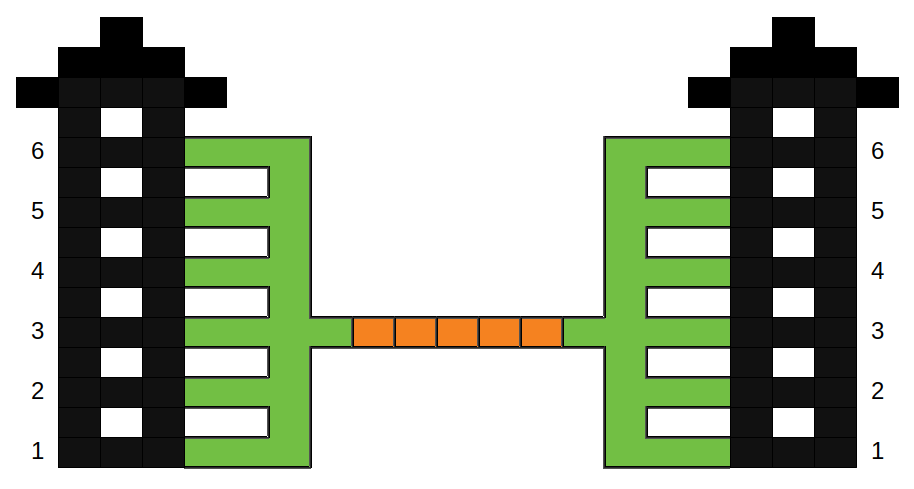
Según las restricciones:
- El piso
del edificio antiguo solo se puede trasladar a los pisos
o
del nuevo edificio.
- El piso
del edificio antiguo solo se puede trasladar a los pisos
o
del nuevo edificio.
- El piso
del edificio antiguo se puede trasladar a cualquier piso del edificio nuevo.
- El piso
del edificio antiguo solo se puede trasladar a los pisos
o
del nuevo edificio.
- El piso
del edificio antiguo solo se puede trasladar a los pisos
o
del nuevo edificio.
- El piso
del edificio antiguo solo se puede trasladar a los pisos
o
del nuevo edificio.
Ejemplo de entrada 2
6 2
1 4
1 1 2 2 2 2
2 2 1 2 1 2Ejemplo de salida 2
0Explicación del ejemplo 2
Este ejemplo se ilustra con la siguiente imagen.
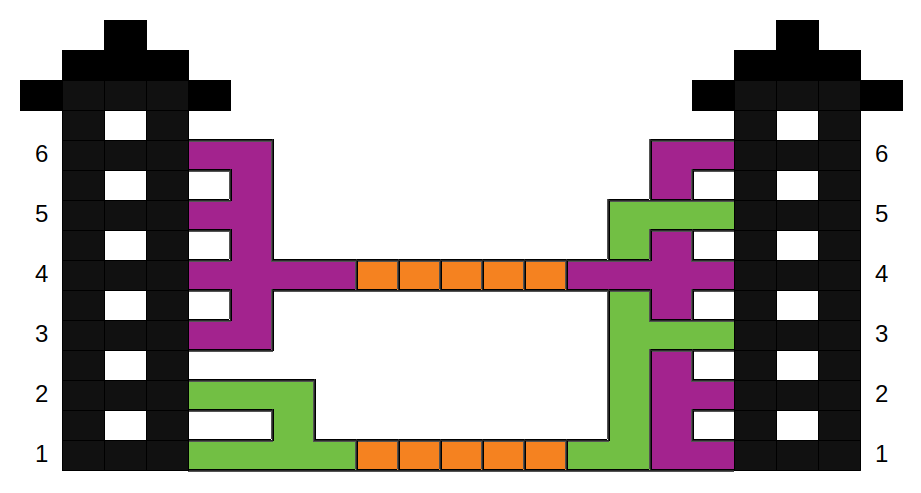
Observe que el piso del edificio antiguo está conectado a un puente aéreo a la altura del piso
(el piso es más alto que el puente aéreo), pero solo los pisos 3 y 5 del nuevo edificio están conectados al puente aéreo (que también son más altos que el puente aéreo). En este caso, el piso 2 no se puede reubicar en ningún lugar sin violar las restricciones. Por tanto, no hay permutación posible.
Comments