Joven Club
Al Palacio Central de los Joven Club de cierta provincia del país llega la encomienda por parte de la Dirección de Educación de crear un pequeño carro inteligente para el uso y disfrute de los niños en círculos de interés de robótica.

El carrito va a funcionar sobre una mesa y no se puede caer por el borde. Se debe tener en cuenta que el mismo no cuenta con sensor de proximidad, por lo tanto, solo se conocen las posiciones donde él puede detenerse gracias a un obstáculo. La mesa puede ser representada por una cuadrícula con filas horizontales y
columnas verticales. Sean
el cuadrado en la
-ésima fila desde arriba y
-ésima columna desde la izquierda. A la mesa se le pueden colocar
obstáculos. El
-ésimo obstáculo se coloca en
. En cada movimiento el carrito debe decidir una de las cuatro direcciones, arriba, abajo, izquierda o derecha, y sigue moviéndose hasta que choca con un obstáculo. Cuando golpea un obstáculo, se detiene en el cuadrado justo antes del obstáculo. Queda prohibido iniciar un movimiento en el que nunca chocará con un obstáculo para evitar su caída. El carrito está inicialmente en
. Se desea que haga una serie de movimientos para detenerse en
. Encuentre el número mínimo de movimientos requeridos para terminar en
. Si no es posible, denunciar el hecho.
Restricciones
- Si
, entonces
.
Todos los valores en la entrada son enteros.
Entrada
La entrada se proporciona desde la entrada estándar con el siguiente formato:
Salida
Imprime el número mínimo de movimientos requeridos para terminar en . Si es imposible terminar allí, imprima
.
Ejemplo #1 de Entrada
7 8 7
3 4
5 6
1 4
2 1
2 8
4 5
5 7
6 2
6 6Ejemplo #1 de Salida
4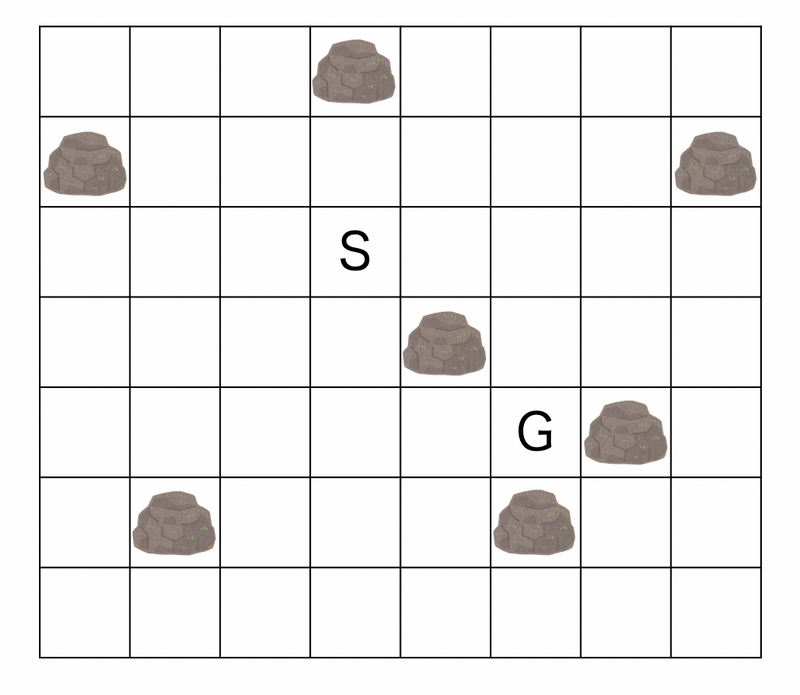
En la figura, están representado por
y
por
.
Al moverse como
, puede terminar en
con 4 movimientos.
Ejemplo #2 de Entrada
4 6 2
3 2
3 5
4 5
2 5Ejemplo #2 de Salida
-1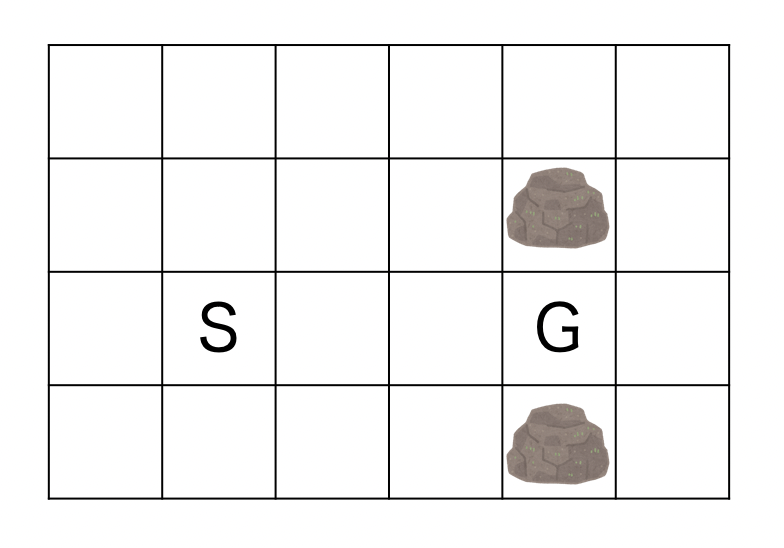
El tiene que parar en . Tenga en cuenta que simplemente pasar por
no se considera que termina en la meta.
Ejemplo #3 de Entrada
1 10 1
1 5
1 1
1 7Ejemplo #3 de Salida
-1
Si elige moverse hacia la izquierda, el carrito caerá por el borde de la mesa después de atravesar .
Tenga en cuenta que está prohibido iniciar un movimiento en el que nunca chocará con un obstáculo, ya que el carrito caería por el borde de la mesa.
Comments