Dado un árbol no dirigido ponderado de ~n~ vértices y una lista de ~q~ actualizaciones. Cada actualización cambia el peso de una arista. La tarea es generar el diámetro del árbol después de cada actualización.

La distancia entre dos vértices es la suma de los pesos en el único camino simple que los conecta. El diámetro es la mayor de todas esas distancias.

Subtareas

• Subtarea 1 (11 puntos): ~n,q \le 100~, ~w \le 10000~.
• Subtarea 2 (13 puntos): ~n,q \le 5000~, ~w \le 10000~.
• Subtarea 3 (7 puntos): ~w \le 10000~ y las aristas del árbol son exactamente todas las aristas válidas de la forma ~(1,i)~.
• Subtarea 4 (18 puntos): ~w \le 10000~ y las aristas del árbol son exactamente todas las aristas válidas de la forma ~(i,2 \cdot i)~ y ~(i,2\cdot i+1)~.
• Subtarea 5 (24 puntos): Se garantiza que después de cada actualización el camino simple más largo pasa por el vértice ~1~.
• Subtarea 6 (27 puntos): Sin restricciones adicionales.

Entrada

La primera línea de la entrada contiene tres enteros separados por espacio ~n~, ~q~ y ~w~ (~2\le n \le 10^5~, ~1\le q \le 10^5~, ~1 \le w\le 2 \cdot 10^{13}~): el número de vértices en el árbol, el número de actualizaciones y el límite de los pesos de las aristas. Los vértices son numerados desde ~1~ hasta ~n~.

Le siguen ~n-1~ líneas que describen el árbol inicial. La ~i~ésima de estas líneas contiene tres enteros ~a_i~, ~b_i~, ~c_i~ (~1 \le a_i, b_i \le n~, ~0 \le c_i < w~): inicialmente hay una arista entre los vértices ~a_i~ y ~b_i~ con peso ~c_i~. Está garantizado que estas ~n-1~ líneas describen un árbol.

Finalmente, ~q~ líneas que describen las actualizaciones como sigue. La ~j~ésima de estas líneas contiene dos enteros separados por espacio ~d_j~, ~e_j~ (~0 \le d_j < n - 1~, ~0 \le e_j < w~). Estos enteros son transformados usando el siguiente procedimiento:

• ~d'_j = (d_j + last) \mod (n - 1)~
• ~e'_j = (e_j + last) \mod (w)~

donde ~last~ es el resultado de la última pregunta (inicialmente ~last=0~). ~(d'_j, e'_j)~ representa una actualización que toma la arista (~d'_j + 1~) de la entrada y actualiza su peso con ~e'_j~.

Salida

Imprime ~q~ línea. La ~i~ésima línea contiene el diámetro del árbol después de la ~i~ésima actualización.

Ejemplos

Entrada 1

4 3 2000
1 2 100
2 3 1000
2 4 1000
2 1030
1 1020
1 890

Salida 1

2030
2080
2050

La imagen de la izquierda muestra el estado inicial del gráfico. Cada imagen siguiente muestra la situación después de una actualización. El peso del borde actualizado está pintado de verde y el diámetro es de rojo.

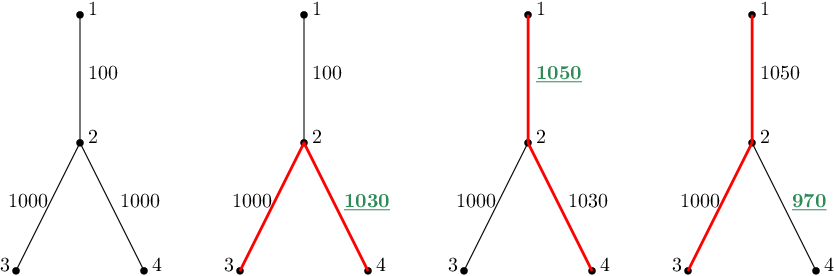
La primera actualización cambia el peso de la ~3~ra arista, es decir, ~(2,4)~ a ~1030~. La distancia más grande entre cualquier par de vértices es ~2030~.

Como la respuesta es ~2030~, la segunda pregunta es:

$$\displaystyle d'_2 = (1 + 2030) \bmod 3 = 0$$ $$\displaystyle e'_2 = (1020 + 2030) \bmod 2000 = 1050$$

De ahí el peso de la arista ~(1,2)~ se cambia a ~1050~. Esto hace que el diámetro sea ~2080~.

Entrada 2

10 10 10000
1 9 1241
5 6 1630
10 5 1630
2 6 853
10 1 511
5 3 760
8 3 1076
4 10 1483
7 10 40
8 2051
5 6294
5 4168
7 1861
0 5244
6 5156
3 3001
8 5267
5 3102
8 3623

Salida 2

6164
7812
8385
6737
6738
7205
6641
7062
6581
5155