Llamamos a un polígono como un polígono con lados consecutivos perpendiculares y las longitudes de los lados con números naturales distinto de cero. Un polígono recto con ~N~ lados se describe mediante una cadena de ~N~ enteros distintos de cero en los que las longitudes de los lados están dadas por el valor absoluto de los números en la cadena, y el signo especifica la posición de los lados, un número positivo significando un lado hacia la derecha o hacia arriba desde la extremidad del lado anterior, y un número negativo para significar el borde hacia la izquierda o hacia abajo de la extremidad del lado anterior; por ejemplo la cadena ~1, 1, -1, -1~ representa un cuadrado del lado ~1~ (el primer lado a la derecha, el segundo arriba, el tercero a la izquierda, el cuarto abajo).

Consideraremos los lados como horizontales o verticales, el primero en el giro indicado es horizontal a la derecha, si el número es positivo, o a la izquierda, si el número es negativo.

Tarea

Se dan una o más cadenas enteras distintas de cero.

• 1 Determinar, para cada uno de ellas, si representa un polígono recto.
• 2 Sabiendo que las filas dadas representan polígonos rectos, determine el área de cada una de ellas.

Especificación de la Entrada

La entrada estándar contiene en la primera línea, separada por espacio, un número natural C y un número natural T. Las siguientes ~2 * T~ líneas describirán las pruebas, dos líneas para cada caso de prueba. Hay un número natural en la primera línea que corresponde a un caso de prueba N, y en la segunda línea una cadena de N enteros, separados por un espacio.

Especificación de la Salida

La salida estándar contendrá en una sola línea los resultados correspondientes a las ~T~ pruebas, separados por un espacio. Si ~C = 1~ para cada fila, el resultado es ~1~, si representa un polígono recto o ~0~ de lo contrario. Si ~C = 2~ para cada fila, el resultado es el área del polígono recto. Ten en cuenta de no haber un espacio demás en la salida.

Restricciones y especificaciones

• ~1 \le T \le 10~
• ~4 \le n \le 100~
• Para casos de pruebas para el ~45~ % de los puntos ~C = 1~, para el resto 55 % de los puntos ~C = 2~.
• Para casos el ~30~ % de los puntos si ~C = 1~ y los números que describen la figura son todos pertenecientes al rango [~-100, 100~]
• Para los otros ~15~ % de los puntos y ~C = 1~, los números que describen la figura están en el rango [~-109, 109~]
• Para los casos con un valor de ~33~ % puntos, para ~C = 2~ y la intersección entre cualquier horizontal con el polígono está vacía o consiste en un solo segmento.
• Para los casos donde el valor de ~C = 2~, los números en la cadena que describe el polígono son enteros distintos de cero en el rango [~-100, 100~] y se garantiza que estas líneas representan polígonos rectos.
• En un polígono recto, los lados no tienen puntos comunes, excepto los extremos de los lados adyacentes.
• El primer y el último lado de un polígono recto son perpendiculares.

Ejemplos #1 de Entrada

1 2
8
5 3 -3 -1 2 -1 -4 -1
8
-2 1 3 1 -4 -3 2 1

Ejemplos #1 de Salida

1 0

Explicación del Ejemplo #1 de Salida

Las cadenas describen las siguientes figuras:

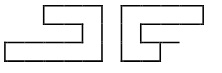
Ejemplos #2 de Entrada

2 2
8
5 3 -3 -1 2 -1 -4 -1
4 
1 1 -1 -1

Ejemplos #2 de Salida

9 1