Sora ha descubierto su nuevo pasatiempo luego de tomar prestado un frisbee de la IOI de Egipto y comenzar a jugar con él. Por desgracia, no puede evitar lanzar el frisbee en dirección a las copas de cristal de su casa, por lo que siempre terminará rompiendo algunas de ellas. Por esa razón, quiere hacer algo para que su madre no se dé cuenta de los daños ocasionados por él. Sora piensa que su madre solo recordará la copa más costosa, por lo que inmediatamente irá a buscar una copa idéntica.

En la casa de Sora hay ~N~ copas de cristal. Las copas están numeradas desde ~1~ hasta ~N~. La copa ~i~ (~1 \le i \le N~) es vendida en una tienda a distancia ~D_i~ de la casa de Sora y tiene un costo ~C_i~. La distancia (en metros) puede variar en dependencia de la disponibilidad de la copa; lo mismo pasa con el costo (en pesos), que puede variar dependiendo de la oferta y la demanda.

Como Sora quiere llegar lo más pronto posible a la tienda, tendrá que tomar un taxi. En la ciudad donde vive Sora todos los taxis tienen una tarifa de ~T~ pesos por metro. Por lo tanto, el costo total de la copa ~i~ (~1 \le i \le N~) será ~D_i \times T + C_i~ pesos. Por desgracia para Sora esa tarifa puede ir aumentando con el tiempo.

Las copas en la casa de Sora están organizadas de una forma muy peculiar: en forma de árbol, donde la copa ~1~ es la raíz. Cada copa, excepto la raíz, tiene un único padre. Específicamente, para cada ~i~ (~1 \le i \le N~) el padre de la copa ~i~ es la copa ~P_i~. Además, asumimos que ~P_1 = -1~.

Para cada copa ~i~ (~1 \le i \le N~), el subárbol de ~i~ es el conjunto conformado por las siguientes copas:

• ~i~, y
• cualquier copa cuyo padre sea ~i~, y
• cualquier copa tal que el padre de su padre sea ~i~, y
• cualquier copa tal que el padre del padre de su padre sea ~i~
• y así sucesivamente.

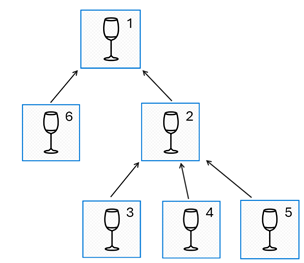
La siguiente figura muestra un ejemplo de un árbol de copas con ~N = 6~. Cada flecha conecta una copa a su padre, excepto para la raíz que no tiene padre. El subárbol de la copa ~2~ está conformado por las copas ~2~, ~3~, ~4~ y ~5~. El subárbol de la copa ~1~ está conformado por todas las ~6~ copas del árbol. El subárbol de la copa ~4~ está conformado solamente por la copa ~4~.

Sora conoce que si el frisbee impacta en una copa ~i~, todas las copas en el subárbol de ~i~ se romperán. Su tarea es escribir un programa que maneje un total de ~Q~ actualizaciones y consultas dadas en el siguiente formato:

• ~1~ ~i~ ~d~ ~c~ ~-~ actualizar la distancia y el costo de la copa ~i~; después de esta actualización ~D_i = d~ y ~C_i = c~.
• ~2~ ~t~ ~-~ aumentar la tarifa de taxi en ~t~; después de esta actualización ~T = T + t~.
• ~3~ ~i~ ~-~ responder con la copa más costosa que se rompería si el frisbee impactara en la copa ~i~.

Entrada

La primera línea de la entrada contiene tres enteros ~N~, ~Q~ y ~T~ ~-~ la cantidad de copas de cristal en la casa de Sora, la cantidad de preguntas y la tarifa inicial de los taxis, respectivamente.

La segunda línea de la entrada contiene ~N~ enteros ~D_1, D_2, \ldots, D_N~ ~-~ la distancia desde la casa de Sora a la tienda donde venden la copa ~i~.

La tercera línea de la entrada contiene ~N~ enteros ~C_1, C_2, \ldots, C_N~ ~-~ el costo de comprar la copa ~i~ en la tienda.

La cuarta línea de la entrada contiene ~N~ enteros ~P_1, P_2, \ldots, P_N~ ~-~ el padre de la copa ~i~. Se garantiza que la forma en que están organizadas las copas es un árbol, y la raíz es la copa ~1~.

Las siguientes ~Q~ líneas son de tres tipos:

• ~1~ ~i~ ~d~ ~c~ (~1 \le i \le N~, ~0 \le d \le 10^6~, ~0 \le c \le 10^6~) ~-~ debes actualizar la distancia y el costo de la copa ~i~.
• ~2~ ~t~ (~1 \le t \le 10^6~) ~-~ debes aumentar la tarifa de taxi en ~t~.
• ~3~ ~i~ (~1 \le i \le N~) ~-~ debes responder con la copa más costosa que se rompería si el frisbee impactara en la copa ~i~.

Salida

La salida debe contener la respuesta a las preguntas de tipo ~3~, en el orden en que fueron dadas.

Restricciones

• ~1 \le N \le 2 \cdot 10^5~
• ~1 \le Q \le 10^5~
• ~0 \le T \le 10^6~
• ~P_1 = -1~; ~1 \le P_i \le N~ para cada ~i~ tal que ~2 \le i \le N~
• ~0 \le D_i \le 10^6~
• ~0 \le C_i \le 10^6~

Subtareas

Subtarea	Restricciones Adicionales	Puntos	Dependencias
~1~	~Q \le 2000~; ~N \le 2000~	~10~	~-~
~2~	~Q \le 100~; ~P_i = i - 1~ para cada ~i~ tal que ~2 \le i \le N~	~5~	~-~
~3~	~P_i = i - 1~ para cada ~i~ tal que ~2 \le i \le N~; En todo momento ~C_i = 0~ para cada ~i~ tal que ~1 \le i \le N~	~7~	~-~
~4~	~P_i = i - 1~ para cada ~i~ tal que ~2 \le i \le N~; No hay actualizaciones de tipo ~2~	~7~	~-~
~5~	~P_i = i - 1~ para cada ~i~ tal que ~2 \le i \le N~	~11~	~2-4~
~6~	En todo momento ~C_i = 0~ para cada ~i~ tal que ~1 \le i \le N~	~10~	~3~
~7~	No hay actualizaciones de tipo ~2~	~10~	~4~
~8~	~-~	~40~	~1-7~

Ejemplos

Entrada 1

4 5 8
7 8 3 10
1 7 1 4
-1 3 1 3
3 1
2 3
1 1 1 4
1 4 8 0
3 2

Salida 1

84
95

Inicialmente ~T = 8~, ~D = [7, 8, 3, 10]~ y ~C = [1, 7, 1, 4]~:

• En la primera consulta se rompen las copas ~S = \{1,3,2,4\}~, y la respuesta es ~\max_{i \in S} (D_i \times T + C_i) = 84~
• Después de la primera actualización, ~T = 8 + 3 = 11~
• Después de la segunda actualización, ~D = [1, 8, 3, 10]~ y ~C = [4, 7, 1, 4]~
• Después de la tercera actualización, ~D = [1, 8, 3, 8]~ y ~C = [4, 7, 1, 0]~
• En la segunda consulta se rompe la copa ~2~, y la respuesta es ~D_2 \times T + C_2 = 8 \times 11 + 7 = 95~

Entrada 2

9 11 6
2 8 7 9 6 9 5 0 3
10 8 0 9 9 1 5 0 4
-1 1 2 1 1 5 6 7 1
3 6
3 5
3 9
2 7
3 2
1 8 7 5
1 5 5 6
2 9
1 3 1 5
3 7
1 8 0 4

Salida 2

55
55
22
112
159

Entrada 3

2 8 0
4 7
2 5
-1 1
2 1
3 1
2 8
3 2
3 2
2 3
3 2
2 1

Salida 3

12
68
68
89