Sekai está jugando un nuevo videojuego del género Tower Defense, donde el objetivo es evitar que los enemigos lleguen a la base principal. El mapa del juego contiene ~N~ ubicaciones. Las ubicaciones están numeradas desde ~1~ hasta ~N~. Hay ~N - 1~ carreteras en el mapa, numeradas desde ~1~ hasta ~N-1~. Las carreteras son bidireccionales y conectan un par de ubicaciones distintas. Específicamente, para cada ~i~ (~1 \le i \le N-1~) la carretera ~i~ conecta dos ubicaciones distintas ~U_i~ y ~V_i~. Hay a lo más una carretera conectando un par de ubicaciones. Dos ubicaciones son adyacentes si están conectadas por una carretera.

Una secuencia de ubicaciones ~v_0, v_1, \ldots, v_k~ (para ~k \ge 0~) es un camino si para cada par de ubicaciones consecutivas ~v_l~ y ~v_{l+1}~ (para cada ~l~ tal que ~0 \le l < k~) son adyacentes.

Un camino ~v_0, v_1, \ldots, v_k~ conecta los vértices ~v_0~ y ~v_k~. En el mapa dado, todo par de ubicaciones está conectado por algún camino.

Afortunadamente hay ~M~ carreteras que se encuentran bloqueadas. Las carreteras bloqueadas están numeradas desde ~1~ hasta ~M~. Específicamente ~B_k~ (~1 \le k \le M~) es el índice de la ~k-~ésima carretera bloqueada.

Al inicio del juego ocurren los siguientes eventos:

• En ~t = 0~ se generan enemigos en todas las ubicaciones que están conectadas con exactamente una única carretera.
• En ~t = 1~ los enemigos se mueven por las carreteras no bloqueadas hacia la ubicación que los acerca más a la base principal.
• En ~t = 2~ los enemigos vuelven a moverse por las carreteras no bloqueadas siguiendo la misma regla.
• Este proceso se repite cada segundo con los enemigos moviéndose hacia la base (si es posible).

Antes de que inicie la partida, Sekai tiene una fase de preparación en la que puede elegir la ubicación de la base principal.

Si un enemigo llega a la base principal, causa daño a Sekai. Si el daño acumulado supera un umbral, Sekai pierde la partida. Para evitar perder Sekai quiere seleccionar la ubicación de la base de tal forma que se maximice la suma de los tiempos que tardan todos los enemigos en llegar a la base. Esto le dará más tiempo para reforzar las defensas.

Si un enemigo no puede moverse hacia la base debido a carreteras bloqueadas, su tiempo de llegada a la base se considera ~0~, ya que nunca llegará. Tu tarea es computar el valor máximo posible de la suma de los tiempos que tardan los enemigos en llegar a la base principal, asumiendo que esta se coloca en una ubicación óptima.

Entrada

La primera línea contiene dos enteros ~N~ y ~M~ ~-~ el número de ubicaciones en el mapa y el número de carreteras bloqueadas, respectivamente.

Las siguientes ~N - 1~ líneas, la ~i-~ésima de esas líneas contiene dos enteros ~U_i~ y ~V_i~ ~-~ la descripción de la carretera ~i~.

La siguiente línea contiene ~M~ enteros ~B_1, B_2, \ldots, B_M~ ~-~ el índice de la ~k-~ésima carretera bloqueada.

Salida

La salida debe contener un único entero ~-~ el valor máximo posible de la suma de los tiempos que tardan todos los enemigos en llegar a la base principal, asumiendo que esta se coloca en la ubicación óptima.

Restricciones

• ~2 \le N \le 10^5~
• ~0 \le M \le N - 1~
• ~1 \leq U_i, V_i \leq N~ y ~U_i \neq V_i~ para cada ~i~ tal que ~1 \le i \le N - 1~
• ~(U_i, V_i) \neq (U_j, V_j)~ para cada ~i~ y ~j~ tal que ~1 \le i < j \le N - 1~
• Cada par de ubicaciones está conectada por algún camino
• ~1 \le B_k \le N - 1~ para cada ~k~ tal que ~1 \le k \le M~

Subtareas

Subtarea	Restricciones Adicionales	Puntos	Dependencias
~1~	~M = 0~; ~N \leq 5000~	~8~	~-~
~2~	~N \leq 5000~	~11~	~1~
~3~	~|U_i - V_i| = 1~ para cada ~i~ tal que ~1 \le i \le N - 1~	~10~	~-~
~4~	~M = 0~	~34~	~1~
~5~	~-~	~37~	~1-4~

Ejemplos

Entrada 1

7 0
1 2
2 6
2 5
3 2
3 4
3 7

Salida 1

11

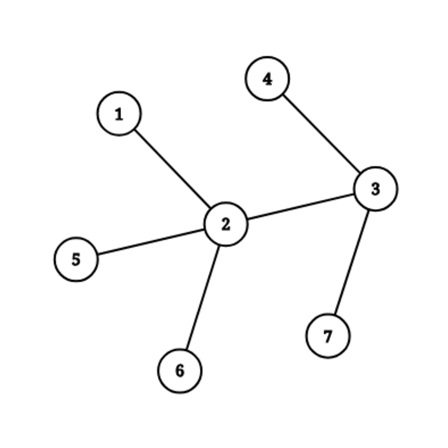
Las ubicaciones conectadas con una sola carretera son: ~[1, 4, 5, 6, 7]~.

Si se ubica la base principal en ~7~, los tiempos para llegar desde las ubicaciones ~[1, 4, 5, 6, 7]~ hasta la base principal son ~[3, 2, 3, 3, 0]~, respectivamente; todos los enemigos en estas ubicaciones pueden llegar a la base principal. La suma de los tiempos es ~3 + 2 + 3 + 3 + 0 = 11~.

También es óptimo ubicar la base principal en ~4~.

Entrada 2

6 1
2 3
3 5
2 4
2 6
2 1
1

Salida 2

4

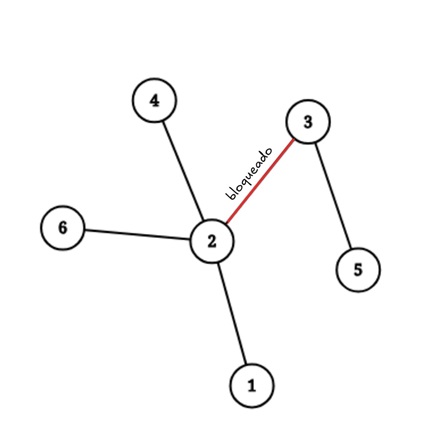
Las ubicaciones conectadas con una sola carretera son: ~[1, 4, 5, 6]~.

Si se ubica la base principal en ~1~ los tiempos para llegar desde las ubicaciones ~[1, 4, 5, 6]~ hasta la base principal son ~[0, 2, 0, 2]~, respectivamente. Nótese que el tiempo requerido para llegar de ~5~ a ~1~ es ~0~ porque es necesario pasar por la carretera ~<2,3>~ que está bloqueada y el enemigo nunca llegará.