El vecindario pastoral del Granjero John (GJ) tiene ~N~ granjas ~(2 \leq N \leq 40 000)~, generalmente numerado/etiquetado ~1...N~. Una serie de ~M~ ~(1 \leq M < 40 000)~ caminos horizontales y verticales de diferentes longitudes ~(1 \leq longitud \leq 1000)~ conecta las granjas. Un mapa de estas granjas podría parecerse a la ilustración a continuación en la cual las granjas están etiquetadas ~F1...F7~.

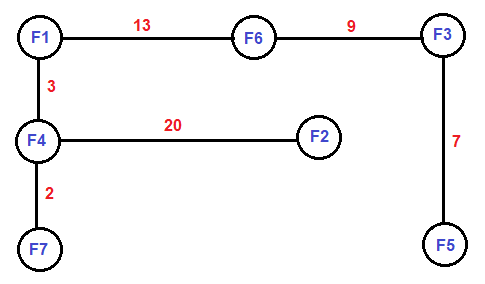
Cada granja puede conectarse directamente a otras cuatro granjas a través de caminos que conducen exactamente al norte, sur, este y/u oeste. Además, las granjas solo son ubicadas en los puntos finales de las carreteras, y se puede encontrar alguna granja en cada punto final de cada camino. No hay dos caminos cruzados, y precisamente un camino (secuencia de caminos) une cada par de granjas.

GJ perdió su copia en papel del mapa de la granja y quiere reconstruirlo de la información de respaldo en su computadora. Esta información contiene líneas como el siguiente, uno para cada camino:

• Hay un camino de longitud ~10~ que corre hacia el norte desde la granja # ~23~ hasta la granja # ~17~
• Hay un camino de longitud ~7~ que corre hacia el este desde la granja # ~1~ hasta la granja # ~17~

Cuando GJ está recuperando estos datos, ocasionalmente lo interrumpe preguntas como las siguientes que recibe de su vecino, el granjero Bob:

• ¿Cuál es la distancia de Manhattan entre las granjas # ~1~ y # ~23~?

GJ responde a Bob cuando puede (a veces todavía no tiene suficiente datos aún). En el ejemplo anterior, la respuesta sería ~17~, ya que Bob quiere saber la distancia "Manhattan" entre el par de granjas. La distancia de Manhattan entre dos puntos ~(x1, y1)~ y ~(x2, y2)~ es solo ~| x1-x2 | + | y1-y2 |~ (que es la distancia que un taxi debe viajar por las calles de la ciudad en una cuadrícula perfecta para conectar dos puntos ~x~, ~y~).

Cuando Bob pregunta por un par de granjas en particular, y GJ aún no puede tener suficiente información para deducir la distancia entre ellos; en este caso, GJ se disculpa profusamente y responde con "~-1~".

Entrada

• Línea 1: Dos enteros separados por espacios: ~N~ y ~M~.
• Líneas 2...M+1: Cada línea contiene cuatro entidades separadas por espacios, ~F1, F2, L~ y ~D~ que describen una carretera. ~F1~ y ~F2~ son números de dos granjas conectadas por una carretera, ~L~ es su longitud y ~D~ es un carácter que es 'N', 'E', 'S' o 'W' dando la dirección de la carretera de ~F1~ a ~F2~.
• Línea M + 2: Un entero, ~K~ ~(1 \leq K \leq 10 000)~, el número de consultas que hace el Granjero Bob.
• Líneas M+3…M+K+2: Cada línea corresponde a una consulta del granjero Bob y contiene tres enteros separados por espacios: ~F1~, ~F2~ e ~I~. ~F1~ y ~F2~ son números de las dos granjas en la consulta y ~I~ es el índice ~(1 \leq I \leq M)~ en los datos después de lo cual Bob pregunta por la consulta. El índice de datos ~1~ está en la línea ~2~ de los datos de entrada, y así sucesivamente.

Ejemplo de Entrada

7 6
1 6 13 E
6 3 9 E
3 5 7 S
4 1 3 N
2 4 20 W
4 7 2 S
3
1 6 1
1 4 3
2 6 6

Detalles de la Entrada

Este es el diseño de la granja dibujado arriba.

Salida

• Líneas 1…K: Un entero por línea, la respuesta a cada una de las consultas de Bob. Cada línea debe contener la medición de la distancia o ~-1~, si es imposible determinar la distancia adecuada.

Ejemplo de Salida

13
-1
10

Detalles de la Salida

En el tiempo ~1~, GJ sabe que la distancia entre ~1~ y ~6~ es ~13~.

En el tiempo ~3~, la distancia entre ~1~ y ~4~ aún se desconoce.

Al final, la ubicación ~6~ es ~3~ unidades al oeste y ~7~ al norte de ~2~, por lo que la distancia es ~10~.