Máximo de Islas.
Siempre que llueve el campo del Bitman termina inundado. Sin embargo, como el campo no está perfectamente nivelado, se llena de agua de una manera no uniforme, y quedan un número de "islas" separadas por extensiones de agua. El campo de Bitman se describe como un paisaje de una sola dimensión especificado por
valores consecutivos de alturas
. Asumiendo que el paisaje está rodeado por muros altos de altura prácticamente infinita, considere qué pasa durante una tormenta: las regiones son cubiertas primero por agua, y se forma un conjunto de "islas" disjuntas, las cuales serán cubiertas todas por agua si el agua continúa elevándose. En el instante en que el nivel del agua sea igual a la altura de un pedazo de tierra, ese pedazo de tierra se considera que está bajo agua.
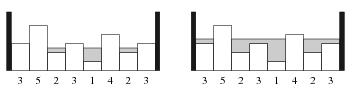
Se muestra un ejemplo de arriba a la izquierda en el que hemos añadido únicamente 1 unidad de agua, lo que deja 4 islas (el máximo que se verá). Más tarde, después de añadir un total de 7 unidades de agua, llegamos a la figura de la derecha con solamente dos islas expuestas. Por favor, calcule el número máximo de islas que veremos en algún momento durante la tormenta hasta que el campo quede totalmente cubierto por agua.
Entrada
La entrada contiene:
- Línea 1: El entero
.
- Líneas 2.. N+1: La línea i+1 contiene la altura
Salida
En una sola línea escribir un solo entero, el número máximo de islas que aparecen en cualquier momento en el transcurso de una tormenta.
Ejemplo de Entrada
8
3
5
2
3
1
4
2
3Ejemplo de Salida
4El ejemplo coincide con la figura mostrada.
Comments