Caminos en la grilla
Hay una matriz con filas horizontales y
columnas verticales. Sea
el cuadrado en la i-ésima fila desde la parte superior y la j-ésima columna de la izquierda.
Para cada
y \(j (1\lei\leH, 1\lej\leW)\), el cuadrado
se describe mediante un carácter
. Si
es \("."\) , el cuadrado
es un cuadrado vacío; si
es \("\#"\), el cuadrado
contiene una pared. Se garantiza que los cuadrados
y
son cuadrados vacíos.
Taro partirá desde Cuadrado y quiere alcanzar
moviéndose repetidamente hacia la derecha o hacia abajo hasta un cuadrado vacío adyacente.
Busque el número de caminos diferentes de Taro desde el cuadrado
a
. Como la respuesta puede ser extremadamente grande, calculela módulo
.
Restricciones:
y
son enteros.
es \("."\) o \("\#"\) .
- Cuadrados
y
son cuadrados vacíos.
Entrada:
La primera línea de entrada contendrá y
.
Luego siguen líneas cada una conteniendo
enteros. El entero en la línea
y la columna
indica
.
Salida:
Imprime el número de caminos de Taro desde Cuadrado
a
, módulo
.
Entrada de ejemplo 1:
3 4
... #
. # ..
....Salida de ejemplo 1:
3Los tres caminos son los siguientes:
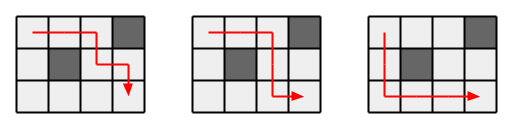
Entrada de ejemplo 2:
5 2
..
#.
..
.#
..Salida de ejemplo 2:
0No hay ningún camino.
Entrada de ejemplo 3:
5 5
..#..
.....
#...#
.....
..#..Salida de ejemplo 3:
24Entrada de ejemplo 4:
20 20
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................
....................Salida de ejemplo 4:
345263555
Comments
El primer caso prueba tiene espacios de mas que podrian confundir.