(Examen clasificatorio de la Olimpiada de Informática CDMX-EDOMEX ciclo 21-22 Nivel 02 Día 2 Problema 3)

Descripción

Karel es un robot con forma de flecha que vive en una matriz rectangular con paredes que no puede atravesar y puede avanzar a sus cuatro direcciones: norte, sur, este y oeste.

Por ejemplo, digamos que Karel empieza en la $1,1$ y hace cuatro movimientos

La matriz consta de una altura $H$ y una base $B$, con torres dentro de este en cada columna; las cuales van desde la base de la matríz hasta una altura determinada que puede ir desde $0$ hasta $H$.

Veamos un ejemplo:

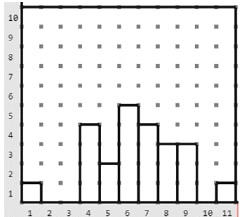
Altura de las torres de izquierda a derecha: $1,0,0,4,2,5,4,2,2,0,1$.
Altura de la matríz: $H=10$; Base de la matríz: $B=11$.

El objetivo de Karel es trasladarse de una casilla inicial a una casilla final. Cada vez que avance se desplazará K casillas hacia la dirección deseada.
Si Karel pasa por la casilla final mientras está avanzando no cuenta como haber llegado a su meta.
Karel debe llegar a la meta sin chocar con las paredes y sin salirse de la matriz.

Problema

Tu tarea es construir un programa que dada la descripción de la matriz, determine si es posible que Karel pueda llegar del punto inicial al final.

Entrada

Primera línea: Dos números $H(1\le H\le {10}^9)$ y $B(1\le B\le 2x{10}^5)$, la altura de la matriz y su base respectivamente. Segunda línea: $B$ números $h_i$ $(0\le hi\le H)$ las alturas de las torres de izquierda a derecha Tercera línea: un número $Q(1\le Q\le 2x{10}^5)$: la cantidad de veces que se le preguntará a Karel si puede llegar de una casilla inicial a una final. Siguientes $Q$ líneas: cinco números: $Yi$, $Xi$, $Yf$, $Xf$, $K(1\le K\le {10}^9)$ que representan respectivamente la coordenada Y inicial, la coordenada $X$ inicial, la coordenada $Y$ final, la coordenada $X$ final y la cantidad $K$ de casillas que debe avanzar ininterrumpidamente en la $q$-ésima pregunta.

La casilla de inicio y fin de cada iteración siempre estará dentro de la matríz y nunca dentro de una torre.

Salida

$Q$ líneas, donde imprimirás "SI" sin comillas si es posible hacer que Karel llegue a la salida y "NO", sin comillas, si no es posible.

Ejemplo

Entrada

11 10
0 0 0 11 0 6 0 0 0 0
6
1 2 1 3 1
2 2 2 3 2
4 3 4 5 2
5 3 11 5 3
6 3 10 5 2
11 10 9 8 2

Salida

SI
NO
NO
NO
NO
SI

Explicación.- En la segunda pregunta. Debe iniciar en el renglón $2$ columna $2$ y terminar en el renglón $2$ columna $3$ y avanzar de $2$ pasos a la vez; pero no hay forma en que Karel pueda llegar con esas condiciones.

En la tercera pregunta: Karel debe iniciar en el renglón $4$ columna $3$ y renglón $4$ columna $5$ con paso dos. Podría llegar dando un paso de tamaño dos a la derecha, pero como hay una pared no puede llegar

En la sexta pregunta (figura 1) Karel podría moverse al oeste (figura 2)y luego al sur; $K=2$ (figura 3) por lo que en cada paso avanza $2$ veces.

figura 1.- Matriz inicial Karel se ubica en el renglón $11$ y columna $10$ y debe llegar al renglón $9$ y columna $8$ y el tamaño del paso es $2$

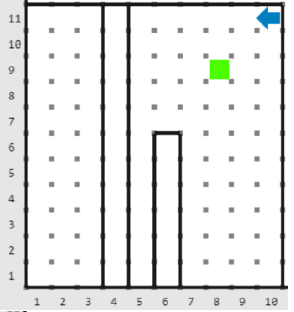
figura 2.- Karel avanzo $1$ paso de $2$ casillas (K=2) hacia el oeste llegando a la posición reglón 11 y columna 8

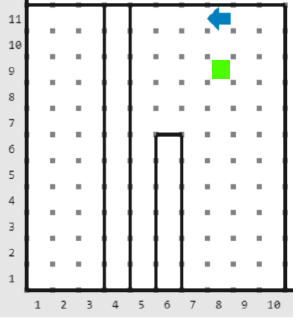
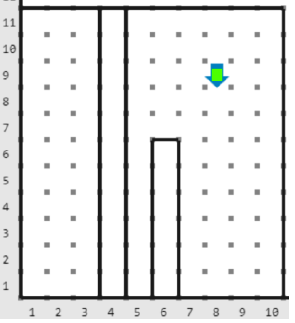
figura 3.- Finalmente Karel da $1$ paso de $2$ casillas (K=2) hacia el sur llegando a su destino en el renglón $.9$ y columna $8$.

Subtareas

Subtarea 1 con un valor de 10 puntos.
No habrá torres en el mundo y $1\le H\le {10}^2$; $1\le B\le 2x{10}^2$;$1\le Q\le {10}^3$.
Subtarea 2 con un valor de 25 puntos.
No habrá torres en el mundo y tendrá los límites originales del problema.
Subtarea 3 con un valor de 35 puntos.
Habrá torres, pero: $1\le H\le {10}^2$; $1\le B\le 2x{10}^2$;$1\le Q\le {10}^3$
Subtarea 4 con un valor de 30 puntos.
$1\le H\le {10}^{9}1\le B\le 2x{10}^5$ o $0\le h_i\le H$ o $1\le Q\le 2x{10}^5$ o $1\le K\le {10}^9$.

NOTA:

Cada subtarea contiene un conjunto de casos de prueba, se te darán los puntos siempre y cuando tu programa resuelva todos los casos de la subtarea.