Estatal 21-22 D2-P2-N02: Deseos
(Examen clasificatorio de la Olimpiada de Informática CDMX-EDOMEX ciclo 21-22 Nivel 02 Día 2 Problema 2)
Descripción
Nati tiene una pulsera formada de cuentas, cada cuenta posee un número positivo o negativo como se
muestra en la figura.
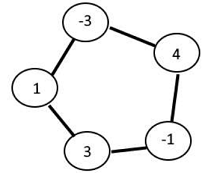
Nati toma una cuenta y empieza a sumar en el sentido de las manecillas de un reloj si durante la suma de las cuentas se obtiene un resultado negativo o la suma total también es negativa, se considera como una Maldición, pero si nunca se obtiene un valor negativo se considera como un deseo.
Ejemplo de una maldición.- Iniciando en la cuenta cuyo valor se tiene que al sumar en el sentido de las
manecillas del reloj
se obtuvo un número negativo y por tanto representa una maldición.
Ejemplo de un deseo.- Iniciando en la cuenta cuyo valor es se tiene:
que equivale a
, si vamos sumando cada cuenta veremos el siguiente detalle.
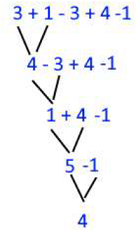
Observando que tanto el resultado final como los intermedios nunca fueron negativos, por tanto se tiene un deseo.
Problema
Tu tarea es construir un programa que dada una pulsera muestre cuantos deseos y maldiciones posee.
Entrada
En la primera línea un valor entero
la cantidad de cuentas en la pulsera.
En la siguiente línea habrá n números enteros llamados
indicado el valor de cada cuenta.
Salida
Dos números enteros, la cantidad de deseos y la cantidad de maldiciones que posee la pulsera.
Ejemplo
Entrada
5
3 1 -3 4 -1Salida
2 3Explicación.- Los dos deseos se forma iniciando en la cuenta con valor
y en la cuenta con valor
. Las
maldiciones se localizan iniciando en las cuentas cuyos valores son
(ya que
),
y
.
Subtareas
Subtarea 1 con un valor de 5 puntos.
Todas las cuentas son valores positivos o negativos y el valor de cada cuenta en el rango de a
.
Subtarea 2 con un valor de 15 puntos.
y el valor de cada cuenta en el rango de
a
.
Subtarea 3 con un valor de 20 puntos.
Solo existe una cuenta negativa y el valor de cada cuenta en el rango de a
.
Subtarea 4 con un valor de 25 puntos.
y el valor de cada cuenta en el rango de
a
.
Subtarea 5 con un valor de 35 puntos.
el valor de cada cuenta en el rango de
a
.
NOTA:
Cada subtarea contiene un conjunto de casos de prueba, se te darán los puntos siempre y cuando tu programa resuelva todos los casos de la subtarea.
Comments
Alguien me puede decir si se necesita algun algoritmo especifico como segment tree para resolver este problema?