Descripción

Alex ha aceptado un trabajo como camarero en las vacaciones de verano. Como le gusta convertir el trabajo de bar en un espectáculo, a veces coloca varios vasos de forma y tamaño idénticos, pero de distinta capacidad, en una pila.

Cada vaso de la pila, excepto el inferior, descansa exactamente sobre dos vasos de la fila inferior. Los vasos están numerados como en la figura de al lado. Los niveles de la pila también están numerados, empezando por el 1 en la parte superior, es decir, el vaso 1 está en el nivel 1, los vasos 2 y 3 están en el nivel 2, los vasos 4, 5 y 6 están en el nivel 3, y así sucesivamente.

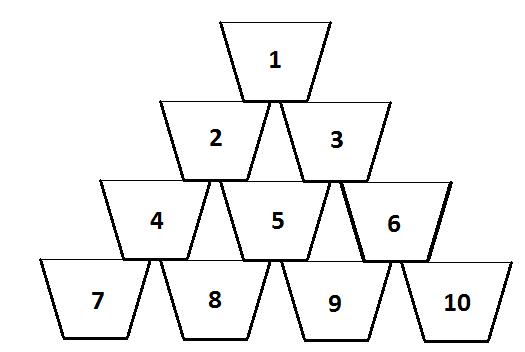
Alex vierte un mililitro de agua (una gota) en el vaso número 1 cada segundo. Los vasos tienen una extraña propiedad cuando están llenos: el primer mililitro que entra en un vaso lleno se escurre instantáneamente en el vaso situado inmediatamente a su izquierda en la fila de abajo, el siguiente mililitro se escurre instantáneamente en el vaso situado inmediatamente a su derecha en la fila de abajo, y así sucesivamente, alternativamente una gota en los dos vasos.

Por ejemplo, cuando el vaso 2 está lleno, el primer mililitro que entra en el vaso 2 pasa al vaso 4, el siguiente mililitro pasa al vaso 5, el tercer mililitro vuelve al vaso 4, y así sucesivamente.

Cuando un nuevo mililitro de agua llega a un vaso lleno en la parte inferior de la pila, se escurre instantáneamente sobre la mesa.

Tarea

Sabiendo el número de vasos que hay en la fila de abajo de la pila y que la pila está llena (todas las filas contienen el número máximo de vasos que se pueden colocar según la regla anterior, y la fila de arriba sólo contiene un vaso), escribe un programa que determine:

1. Cuál es el nivel mínimo (superior) que tiene la suma de las capacidades de todos los vasos del nivel máximo?
2. ¿Cuál es el número mínimo de segundos necesarios para llenar todos los vasos siguiendo el proceso descrito anteriormente, y cuántos mililitros de agua se desperdician (se derraman sobre la mesa) en este caso?

Entrada

En la primera línea del fichero de entrada pic.in hay un número natural V cuyo valor sólo puede ser 1 ó 2.

En la segunda línea del fichero de entrada hay un único número natural N que representa el número de vasos de la fila situada en la parte inferior de la pila.

En la tercera línea del fichero de entrada hay M = N*(N+1)/2 números naturales C1,C2,...,CM separados por un espacio, Ci representando la capacidad (en mililitros) del vaso número i de la pila.

Salida

Si el valor de V es 1 entonces el fichero de salida pic.out contendrá en la primera línea un único número natural que representa el número de orden del nivel mínimo (más alto) que tiene la suma de las capacidades de todos los vasos del nivel máximo.

Si el valor de V es 2 entonces el fichero de salida contendrá en la primera línea dos números naturales separados por un único espacio que representan el número mínimo de segundos transcurridos hasta que todos los vasos de la pila estén llenos y el número de mililitros de agua desperdiciados (alcanzados sobre la mesa) en ese momento.

Restricciones

• 2 ≤ N ≤ 50
• El 20% de las pruebas tendrán V = 1 y el 80% de las pruebas tendrán V = 2.
• El 35% de las pruebas tendrán N ≤ 17 y el 65% de las pruebas tendrán N > 17.
• 1 ≤ C1,C2,...,CM ≤ 25

Ejemplo de Entrada #1

1 
3
2 4 2 1 2 3

Ejemplo de Salida #1

2

Explicación del ejemplo

V = 1, por lo que SÓLO se resuelve el primer requisito.

En el nivel 1 hay un vaso de capacidad 2. En el nivel 2 hay dos vasos de capacidad 4 y 2. En el nivel 3 hay tres vasos de capacidad 1, 2 y 3. La suma de las capacidades de los vasos es: 2 en el nivel 1, 6 en el nivel 2 y 6 en el nivel 3, por lo que el nivel más alto con la suma máxima -6- es el nivel 2.

Ejemplo de Entrada #21

2 
3
2 4 2 1 2 3

Ejemplo de Salida #2

18 4

Explicación del ejemplo

V = 2, por lo que SOLO se resuelve el segundo requisito.

Después de 10 segundos la configuración de los vasos es la siguiente: Vaso Número de gotas Observaciones 1 2 Lleno 2 4 Lleno 3 2 Plin 4 0 5 1 6 1

La undécima gota fluye del vaso 1 al vaso 2 y después al vaso 4.

La siguiente gota fluye del vaso 1 al vaso 3 y más allá al vaso 5 que se llena. y así sucesivamente.

Después de 18 segundos, todos los vasos están llenos, y del vaso 1 se ha desperdiciado una gota, del vaso 2 se han desperdiciado 3 gotas, y del vaso 3 no se ha desperdiciado ninguna gota, por lo que en total se han desperdiciado 4 gotas.