Transformando Palabras
Rafael disfruta numerosas clases de juegos con palabras. Actualmente, él está sumamente interesado en los juegos de transformación de palabras. Esencialmente, dada una palabra (una secuencia consecutiva de caracteres), debe aplicar un conjunto de reglas que especifican cómo debería ser cambiado cada carácter. En particular, está muy interesado en un juego donde sólo se utilizan tres letras ('A', 'B' y 'C'). El conjunto de reglas a aplicar es el siguiente:
A -> AB
B -> AC
C -> AEsto significa que dada una palabra, todas las apariciones del carácter 'A' deberían ser transformadas en 'AB', todas las apariciones de 'B' deberían ser transformadas en 'AC' y todas las apariciones de 'C' deberían ser transformadas en 'A'. Por ejemplo, la palabra 'BCA' se transformaría en 'ACAAB':
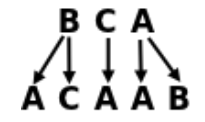
Ahora Rafael considera una secuencia de palabras donde cada palabra se obtiene aplicándole las reglas ya definidas a la palabra anterior de la secuencia. La primera palabra de la secuencia,
, es 'A'. Aplicando las reglas,
es 'AB',
es 'ABAC',
es 'ABACABA' y así siguiendo. La figura a continuación ilustra las transformaciones para estas primeras
palabras de la secuencia:
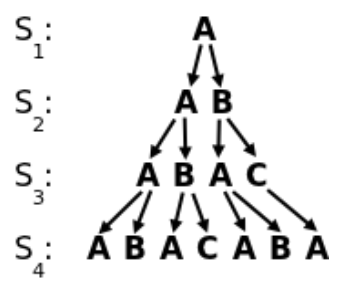
Rafael pensó que la secuencia que obtuvo era realmente bella y no pudo contenerse de calcular más y más palabras de la secuencia. Pero las palabras se hicieron tan largas que se volvió muy difícil hacerlo todo a mano, y necesita ayuda. Él se dio cuenta de que lo que necesita es una manera de calcular cuál es el \(K-ésimo\) carácter en la \(N-ésima\) palabra de la secuencia. Por ejemplo, si es
y
es
, la respuesta que está buscando es 'A', pues el 3er carácter de la 4ta palabra en la secuencia (
= 'ABACABA') es 'A'. Si ambos
y
fueran
, la respuesta sería 'C', ya que el 4to carácter de
es 'C'.
Debes ayudar a Rafael en estos cálculos. Dado un conjunto de enteros y
, debes calcular cuál es el \(K-ésimo\) carácter de la \(N-ésima\) palabra en la secuencia definida anteriormente, esto es, el carácter en la posición
de la palabra
. Notar que
es siempre 'A' y el conjunto de reglas para transformar una palabra es siempre A->AB, B->AC y C->A.
Entrada
La primera línea contiene un único entero
indicando el número de casos que siguen a continuación.
Luego siguen líneas, cada una de ellas describiendo cada caso de prueba. Cada línea contiene dos enteros
y
^
, separados por un único espacio, indicando que debes computar el \(K-ésimo\) carácter de la \(N-ésima\) palabra en la secuencia. Se garantiza que
corresponde a una posición válida, es decir,
contiene al menos
caracteres.
Salida
La salida debería tener exactamente líneas, cada una con un único carácter conteniendo la respuesta a los respectivos casos, esto es, cuál es el carácter en la posición
de la palabra
. Las respuestas deberían darse en el mismo orden que la entrada, es decir, la primera línea de la salida debería ser la respuesta al primer caso de prueba, y así siguiendo.
Ejemplo de Entrada
10
4 3
4 4
2 1
2 2
3 4
5 11
5 8
10 30
8 25
7 20Ejemplo de Salida
A
C
A
B
C
C
A
B
A
A
Comments